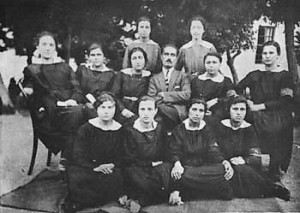Ο σκοπός του σχολείου

«Αγαπήσατε το παιδί, κατεβείτε κοντά του, βάλτε το χέρι σας στην καρδιά του. Αφουγκρασθείτε τον πόνο του και τη χαρά του»

«Σκοπός του σχολείου δεν είναι – δεν πρέπει να είναι – το σοφό παιδί, αλλά το ευτυχισμένο παιδί. Κι αυτό το παιδί μόνο μέσα σε ένα δραστικό κι όχι σκυθρωπό σχολείο μπορεί να ολοκληρωθεί. Η αξία του ανθρώπου δε βρίσκεται στις γνώσεις, αλλά στην ισχυρή βούληση, στην ολοκληρωμένη προσωπικότητα, στην πνευματική καλλιέργεια, στη δημιουργία πλούσιας συναισθηματικής, ζωής, στη μέθεξή τους στην κοινωνική ζωή»

«Οι ψυχές του δασκάλου και του παιδιού βρίσκονται πέρα και πάνω από τη μέθοδο. Όταν αυτές επικοινωνούν, βρίσκουν τη μέθοδο. Διαφορετικά κι ολόκληρο το γνωστικό ουρανό να κατεβάζει ο δάσκαλος, είναι καταδικασμένος σε αποτυχία. Άλλωστε, για τον καλλιτέχνη δάσκαλο ισχύουν οι νόμοι της τέχνης, της δημιουργίας, της φυσικότητας, της εσωτερικής διάθεσης. Αυτοί είναι που του ανοίγουν το δρόμο».

Θεόδωρος Κάστανος (1888-1932)

Ο Διευθυντής Θεόδωρος Κάστανος με τις δευτεροετείς σπουδάστριες του τριταξίου Διδασκαλείου στην αυλή του Αρχιγενείου Διδασκαλέίου Επιβατών (1922).

Κείμενο από την εφημερίδα του Ομίλου Επιμόρφωσης Γονέων (Βροντάδος Χίου) «Τα παιδιά μας κι εμείς» φ. 109 | Κάστανος Θεόδωρος: Ένας μεγάλος παιδαγωγός (παρουσίαση της ζωής του από τον Χρίστο Τσολάκη, καθηγητή της Νεοελληνικής Γλώσσας & της Διδακτικής της στη Παιδ. Σχολή του ΑΠΘ) | Ο Θεόδωρος Κάστανος και το Σχολείο Εργασίας, περιοδικό Ρόπτρο, τεύχος 24, Νοέ. 2008

Η σημασία των οπτικών αναπαραστάσεων ("Minds are visual")

Έχει διαπιστωθεί από σχετικές εργασίες που αφορούν τη γνωστική επιστήμη και τις βιολογικές λειτουργίες που σχετίζονται με τη μάθηση η σημασία των εικόνων για τη μάθηση. (minds are visual όπως χαρακτηριστικά λέγεται). Ο νους αρέσκεται στο να μαθαίνει μέσα από εικόνες (Laughbaum, 2004). Το γεγονός αυτό δικαιολογεί τις δυσκολίες που συναντούν οι μαθητές στη μονοδιάστατη μελέτη της άλγεβρας αποκλειστικά μέσω των αλγεβρικών συμβόλων της. Στον καθένα συμβαίνει να μην μπορεί πολλές φορές να θυμηθεί ούτε καν το τηλέφωνο ενός στενού συγγενή του ενώ την ίδια στιγμή οι εικόνες που μπορεί έχει για το πρόσωπο αυτό στο αποθηκευμένες στο μυαλό του είναι . Το μυαλό μας έχει μια αξιοθαύμαστη ικανότητα να θυμάται εικόνες. Χαρακτηριστικό είναι το σχετικό πείραμα Baker/baker των ψυχολόγων, που δείχνει ότι ευκολότερα μπορεί να θυμηθεί κάποιος ένα ονοματεπώνυμο (Mr. Baker) αν το συνδέσει στο μυαλό του με την εικόνα ενός φούρναρη στην προκειμένη περίπτωση (baker). Δεν χρειάζεται όμως κανείς να ανατρέξει στις επιστημονικές έρευνες για να το διαπιστώσει. Δεν είναι τυχαίο ότι οι μαθητές οι οποίοι απομνημονεύουν για τις εξετάσεις θεωρητικών μαθημάτων μακροσκελή τμήματα ύλης, μπορούν εύκολα να φέρνουν στο μυαλό τους τη μορφή της σελίδας και τα σχήματα και τις εικόνες που περιέχει στο σημείο αυτό στο οποίο χρειάζεται να ανατρέξουν. Κι όμως τις περισσότερες φορές ενώ βρίσκουν δυσκολία να ανακαλέσουν το περιεχόμενο του ίδιου του κειμένου, μπορούν να βοηθηθούν ώστε να ανασυρθεί αμέσως η ζητούμενη πληροφορία αν λίγο βοηθηθούν «μήπως είναι στη σελίδα που έχει το εκείνο ή το άλλο σχήμα;» ή «μήπως είναι ο τύπος που βρίσκεται μέσα στο κίτρινο πλαίσιο;». Τα βιβλία γενικότερα έχουν τις βασικότερες πληροφορίες μέσα σε πλαίσια διαφορετικού χρώματος ή χρησιμοποιούν πιο έντονα τυπογραφικά στοιχεία για να δώσουν έμφαση, βοηθώντας ουσιαστικά τη μνήμη να ανασύρει την πληροφορία αργότερα. Εκεί μάλιστα που δε υπάρχει σχήμα ή διαφορετικό χρώμα, με χρωματιστούς μαρκαδόρους υπογραμμίζουμε ή ζωγραφίζουμε πλαίσια ώστε να ανατρέξουμε αργότερα. Η πλέον κλασσική τεχνική απομνημόνευσης μιας λίστας αντικειμένων για παράδειγμα είναι η σύνδεση των αντικειμένων αυτών (που μπορεί να είναι γράμματα για παράδειγμα ή λίστα για ψώνια) με άλλες γνωστές εικόνες (όπως πχ. αρχικά κυρίων ονομάτων ή θέση στο χώρο του σπιτιού στον οποίο θα τοποθετήσουμε τα αντικείμενα που θα αγοράσουμε, ή το σημείο από το οποίο λείπουν) ή με όρους τμημάτων πληροφορίας που έχει νόημα για μας  (Βοσνιάδου, 2001, σελ. 186). 

Γενικότερα η προϋπάρχουσα γνώση ενισχύεται με την κωδικοποίηση του υλικού σε τμήματα πληροφορίας που έχουν σημασία με βάση τις προηγούμενες γνώσεις.

Και οι εικόνες είναι γνωστές και έχουν νόημα σε όλους γιατί ανήκουν στην καθημερινή μας εμπειρία! Για παράδειγμα αν διαβάσουμε στη σειρά τα γράμματα: ‘Κ Σ Λ Υ Ο Σ Γ Τ Α Α Κ Ρ Α Κ Λ Ε Α’ και προσπαθήσουμε να τα επαναλάβουμε δε θα τα καταφέρουμε, ενώ αν τα ίδια γράμματα τα αναδιατάξουμε στην εξής σειρά ‘ΣΚΥΛΟΣ ΓΑΤΑ ΚΑΡΕΚΛΑ’ τότε είναι πιο εύκολο να τα συγκρατήσουμε. Κι όμως και οι δύο σειρές αποτελούνται από τους ίδιους ακριβώς χαρακτήρες. Τα αποτελέσματα αφορούν τόσο τη βραχυπρόθεσμη μνήμη, όσο και τη μακροπρόθεσμη (Βοσνιάδου 2001, σελ. 187). Άρα όταν προσπαθούμε να μάθουμε κάτι το πετυχαίνουμε καλύτερα όταν η πληροφορία αυτή εξ αρχής κωδικοποιηθεί κατάλληλα ώστε να έχει κάποιο νόημα στα πλαίσια της προϋπάρχουσας γνώσης. Οι άνθρωποι μπορούν να χρησιμοποιήσουν την οπτική κωδικοποίηση για να επεξεργαστούν εικόνες στη μακροχρόνια μνήμη (που είναι και το ζητούμενο για τη μάθηση). Σε μια μελέτη, τα άτομα που συμμετείχαν σε αυτή είδαν 2.500 εικόνες. Αν και χρειαστήκαν 16 ώρες για να παρουσιαστούν τα ερεθίσματα, τα υποκείμενα αργότερα αναγνώρισαν σωστά περισσότερο από το 90% των εικόνων (Standing, Conezio & Haber, 1970). Ένας λόγος που εξηγεί το γεγονός ότι τα υποκείμενα θυμόντουσαν τόσο καλά τις εικόνες είναι ότι τα ερεθίσματα αυτά μπορούν να αναπαρασταθούν και οπτικά και σημασιολογικά. Η θεωρία της διπλής κωδικοποίησης υποστηρίζει ότι θυμόμαστε καλύτερα τις πληροφορίες όταν αυτές αναπαρίστανται και με τους δύο κώδικες παρά μόνο με τον έναν (Paivio, 1986). 

---

• Οπτική κωδικοποίηση: Συνδέουμε κάτι με την εικόνα του (π.χ. θυμόμαστε έναν συγγενή με τα χαρακτηριστικά του).
• Σημασιολογική αναπαράσταση: Συνδέω κάτι με τη λειτουργία του (π.χ. κατανοώ τη μητρική αγάπη ως έννοια).
• Θεωρία της διπλής κωδικοποίησης: Θυμόμαστε καλύτερα τις πληροφορίες όταν αυτές αναπαρίστανται και με τους δύο κώδικες παρά μόνο με τον έναν.
• Αναπτύξτε διαφορετικές αναπαραστάσεις για το ίδιο θέμα:Όσες περισσότερες αναπαραστάσεις (τρόπους) έχουμε για να προσεγγίσουμε κάτι, τόσο καλύτερα το συγκρατούμε στη μνήμη και το κατανοούμε.

Διδασκαλία των μαθηματικών με ηλεκτρονικό υπολογιστή

Κίνηση Μαθηματικά Σωματική άσκηση Πνευματική Περπάτημα Νοερός υπολογισμός «με το μυαλό» (λες και τα υπόλοιπα δεν θέλουν μυαλό για να γίνουν) Ποδήλατο Υπολογισμός με χαρτί και μολύβι Μοτοποδήλατο Calculator, Computer (αυτοματισμός και ευκολία) (Kützler)

Η είσοδος των υπολογιστών έχει ήδη επηρεάσει τα μαθηματικά που διδάσκονται στο σχολείο και τα μαθηματικά που «χρειάζεται» κανείς.

Για παράδειγμα ο αλγόριθμος προσιορισμού της τετραγωνικής ρίζας ενός οποιουδήποτε αριθμού απουσιάζει εδώ και αρκετά χρόνια από την εκπαίδευση αφού πλέον μπορεί κανείς να τον υπολογίσει με τον υπολογιστή τσέπης. Το ίδιο και ο υπολογισμός λογαρίθμων και άλλα θέματα, τα οποία το αναλυτικό πρόγραμμα δεν θεωρεί απαραίτητα να διδαχθούν πλέον...

Τα τεχνολογικά μέσα και οι ανάγκες που δημιουργεί ο πολιτισμός κάθε εποχής υπαγορεύουν τους στόχους, το περιεχόμενο και την κατεύθυνση της εκπαίδευσης. Εξάλλου ποια είναι τα μαθηματικά που χρειάζεται κάποιος; Την απάντηση την διαμορφώνουν οι ίδιες οι ανάγκες και οι τεχνολογικές εξελίξεις της κοινωνίας! (Ξεχνάμε κάποιες φορές οι μαθηματικοί ότι δε θα γίνουν όλοι οι μαθητές συνάδελφοί μας και επομένως δεν χρειάζεται να τα μάθουν όλα με μιας!).

Κάποιοι λένε: «Αν οι προηγούμενες γενιές δεν χρειάστηκαν την τεχνολογία για να μάθουν μαθηματικά, τότε ούτε τα παιδιά μας τη χρειάζονται. Άλλωστε και χωρίς να έχουμε τους υπολογιστές τα καταφέραμε καλά».

Όμως η κοινωνία και οι ανάγκες της κινούνται με βάση την εξέλιξη της τεχνολογίας. Και σύμφωνα με την εξέλιξη της τεχνολογίας κινούνται και τα μαθηματικά κάθε εποχής αλλά και η διδασκαλία τους. Εκπαίδευση και πολιτισμός εξελίσσονται παράλληλα.

Οι υπολογιστές δίνουν την ευκαιρία εκεί που το ενδιαφέρον ήταν αποκλειστικά εστιασμένο στις πράξεις και τις διαδικασίες, να μετατοπιστεί και σε άλλα θέματα των μαθηματικών, που βοηθούν την κατανόηση των εννοιών και των τεχνικών σε βάθος. Εμπλουτίζουν τις εμπειρίες γύρω απο τα μαθηματικά, είναι το κατάλληλο περιβάλλον για κάποιον να «κάνει» μαθηματικά και όχι απλά να ακούσει γι’ αυτά αλλά να εμπλακεί ενεργητικά, δίνοντας την ευκαιρία για πειραματισμό, παρατήρηση, συμπέρασμα και δικαιολόγηση όπως υπαγορεύει η σύγχρονη Διδακτική μεθοδολογία.

Μάθηση: Η οργάνωση της μνήμης

«Σκέψη είναι η κίνηση της μνήμης... και μνήμη είναι εμπειρίες και γνώσεις αποθηκευμένες στον εγκέφαλο». Σε αυτό είχαν συμφωνήσει ο διάσημος φυσικός Ντέιβιντ Μπομ και ο γνωστός ινδός δάσκαλος Τζίντου Κρισναμούρτι από το 1980.

---

Η μάθηση είναι η ουσία της δουλειάς του εκπαιδευτικού. Όμως τι είναι η μάθηση; Πώς μαθαίνουμε;

Μια θεωρία που περιγράφει τη λειτουργία της σκέψης και το πώς είναι οργανωμένη η μακροπρόθεσμη μνήμη, είναι η θεωρία σημασιολογικών δικτύων. Οι θεωρία αυτή ότι οι πληροφορίες είναι οργανωμένες σε μορφή δένδρων στα οποία κάθε κόμβος αποτελεί τη συγκεκριμένη πληροφορία. Οι δεσμοί (μονοπάτια) είναι οι συνδέσεις μεταξύ τους. Μπορούμε να το φανταζόμαστε με την οργάνωση των αρχείων στο σκληρό δίσκο ενός ηλεκτρονικού υπολογιστή, με τη σημαντική όμως διαφορά ότι υπάρχουν απεριόριστες δυνατότητες σύνδεσης μεταξύ των πληροφοριών ώστε να μπορούμε να πηγαινοερχόμαστε από τη μία στην άλλη σκέψη μέσα στο μυαλό μας.

Για παράδειγμα, αν ρωτήσουμε κάποιον αν η πρόταση «το χελιδόνι είναι πουλί», είναι αληθής ή ψευδής, οι έννοιες πουλί και σπουργίτης θα ενεργοποιηθούν και η εξαπλούμενη ενεργοποίηση από κάθε έννοια θα αρχίσει να διασχίζει όλα τα μονοπάτια του δικτύου που σχετίζονται με την έννοια ώστε η ενεργοποίηση και από τις δύο έννοιες να συναντηθούν στο κέντρο του μονοπατιού. Κάποια ευρύτερα τμήματα του δικτύου μπορεί να συνδέονται μεταξύ τους διαμορφώνοντας ευρύτερες γνωστικές περιοχές (γνωστικά σχήματα) και αυτές να συνδέονται με άλλες κ.ο.κ.

Η ποσότητα και η ποιότητα της γνώσης καθορίζεται από την ποσότητα των πληροφοριών και την πολυπλοκότητα και το πλήθος των ζεύξεων μεταξύ τους.

Κάποιες συνδέσεις μέσα στο δίκτυο μπορεί να είναι λιγότερο ισχυρές από κάποιες άλλες. Μπορούμε τα μονοπάτια αυτά να τα φανταζόμαστε ότι έχουν μεγαλύτερο πάχος από τα υπόλοιπα. Στα μονοπάτια λεπτού πάχους η εξαπλούμενη ενεργοποίηση ταξιδεύει πιο αργά από ότι στα μονοπάτια που αποτελούν ισχυρότερες συνδέσεις και μάλιστα μπορεί αν οι ζεύξεις δεν είναι αρκετά ισχυρές δύο κόμβοι (δηλαδή δύο πληροφορίες της μακροπρόθεσμης μνήμης) να είναι τελικά ασύνδετοι μεταξύ τους. Είναι η περίπτωση έλλειψης κατανόησης.

---

• Γνωστικό σχήμα: Μια θεματική περιοχή. Μπορεί να είναι ολόκληρη θεωρία (π.χ. τα μαθηματικά) ή μια επιμέρους υποπεριοχή (η έννοια της συνάρτησης, ή η παραγοντοποίηση στην άλγεβρα).
• Μάθηση: Στόχος είναι να συνδέσουμε στο μυαλό του μαθητή τις έννοιες μεταξύ τους.
• Έλλειψη κατανόησης: Ασύνδετα γνωστικά σχήματα ή ασθενείς δεσμοί μεταξύ τους.

Ημερίδα για το νέο βιβλίο της Άλγεβρας Α' Λυκείου

- 'Ιδιο εξώφυλλο με το παλιό αλλά πιο καλογραμμένο και πιο απαιτητικό όπως φαίνεται το νέο βιβλίο.

- Δεν είναι μέθοδος διδασκαλίας άνευ διδασκάλου. Επομένως ο δάσκαλος θα αποφασίσει για το ποια σημεία θα αφήσει απ' έξω ανάλογα με τους μαθητές που έχει από κάτω. Άλλωστε δεν θα προλάβει να τα πει όλα.

- Έμφαση στις γραφικές παραστάσεις και τη γεωμετρική εποπτεία με χρήση Η/Υ (Sketchpad & Geogebra).

- Οι προσεγγιστικές μέθοδοι έχουν αφοριστεί από τα μαθηματικά στο ελληνικό σχολείο. Όμως έχουν θεμελιώδη ρόλο στην σύγχρονη έρευνα και τεχνολογία. Και τη στιγμή που στο εξωτερικό οι επιστημονικές διατριβές οδηγούν τις εξελίξεις, εμείς εδώ προσπαθούμε να δείξουμε ότι το 1 > 0 (σε σημείο που θα ενοχλούσε και τον ίδιο τον Πλάτωνα). Θέλουμε να πούμε με αυτό ότι υπάρχουν και οι γραφικές επιλύσεις των συστημάτων. Ναι! Τελικά το 2.19 είναι κι αυτό ένα πολύ καλό νούμερο - γιατί όχι;!